Síkidomok, sokszögek 1.
Feladat
Mindannyian szeretjük, ha a nevünkön szólítanak bennünket.
A sokszögek esetében sincs ez másképp. Ezzel a programmal megtanulhatod, begyakorolhatod, melyik sokszöget hogyan hívják, milyen tulajdonságok alapján lehet őket csoportosítani.
Húzd a táblázatban található név alatti mezőbe a neki megfelelő sokszöget!
A rajzlapon különböző konvex és konkáv sokszög látható. Ezek alatt egy táblázat, benne a sokszögek neve. A kiválasztott sokszög belsejébe kattintva az alakzata kívánt helyre húzható. Az ellenőrzés BE gomb hatására a jó helyre húzott sokszögek kék színűre változnak. Piros színűre változnak azok, amelyek rossz helyre kerülnek. A „mutat” (
) gomb önálló ellenőrzésre, az „Újra” (
) gomb az eredeti állapot visszaállítására való.
A munkalap teljes megjelenítéséért kattintson a „Teljes képernyő” ( 
) gombra az oldal jobb felső sarkában
Segítség a tanulónak a feladatmegoldáshoz - videómagyarázat
Segítség a tanulónak a feladatmegoldáshoz - szöveges tananyag
Síkbeli alakzatok, sokszögek
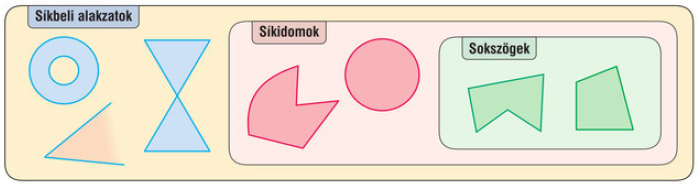
A síkbeli alakzatok csoportosítása
Ha egy síkbeli alakzat végtelen, vagy lyukas, vagy egy pontját elvéve szétesik, akkor nem síkidom.
A síkidomokat görbe és egyenes vonalak is határolhatják.
A sokszögek a szakaszokkal határolt síkidomok.
A síkidomokat nem csupán a határoló vonalak szerint csoportosíthatjuk, hanem aszerint is, hogy a síkidom két pontját összekötő szakasz hol halad. Így a síkidomok lehetnek konvex vagy nem konvex alakzatok.
Konvex síkidomok
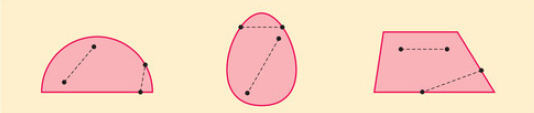
Konvex az a síkidom, amelynek bármely két pontját összekötő szakasznak minden pontja a síkidomhoz tartozik.
Nem konvex síkidomok
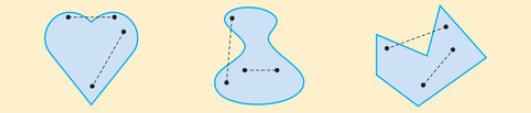
Nem konvex (azaz konkáv) az a síkidom, amelynek van két olyan pontja, amelyeket összekötő szakasznak nem minden pontja tartozik a síkidomhoz.
A sokszögek
A sokszöget határoló szakaszok az oldalak (a, b, c, d, e).
Két oldal közös végpontját csúcsnak (A, B, C, D, E), egy oldal két végpontját szomszédos csúcsoknak (pl. A és B) nevezzük.
Két nem szomszédos csúcsot összekötő szakasz az átló (pl. DB átló).
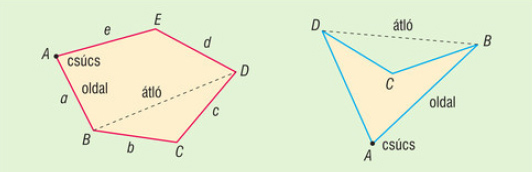
A sokszögeket oldalaik száma alapján is osztályozhatjuk.
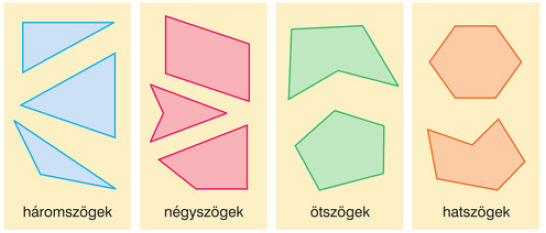
Egy sokszögben a csúcsok száma megegyezik az oldalak számával.
Interaktív feladat
Utolsó módosítás: 2019. March 26., Tuesday, 23:56