9. évfolyam
Nagy számok törvénye 1
Szükséges előismeret
Binomiális eloszlás. Várható érték, szórás.
Módszertani célkitűzés
A binomiális eloszlás várható értékétől való eltérések becslése. A szórás és a valószínűség közötti kapcsolat.
Az alkalmazás nehézségi szintje, tanárként
Nehéz (érdemes előre megismerni a teljes anyagot).
Felhasználói leírás
FELADAT FELVEZETÉSE Egy véletlen kísérlet abból áll, hogy egy szabályos pénzérmét 100-szor feldobunk. Az Alkalmazás grafikusan mutatja azokat a valószínűségeket, amelyeket a kísérlet során dobható fejek száma alapján kaphatunk.
A véletlen kísérlet végrehajtása előtt mire érdemes inkább fogadni: arra, hogy 0-tól 49-ig lesz a dobott fejek száma (50 különböző lehetséges eredmény), vagy arra, hogy ez a szám 47 és 53 között lesz (7 különböző lehetséges eredmény)?
DIÁKOKNAK SZÓLÓ BEVEZETŐ KIEGÉSZÍTÉSE
Arra érdemesebb fogadni, hogy 47 és 53 között lesz a fejek száma, hiszen ennek valószínűsége 0,5-nél nagyobb, míg a 0 és 49 közötti esetek összege nem éri el a 0,5-öt.
Kérdések, megjegyzések, feladatok
FELADAT
Legalább 95%-os valószínűséggel milyen tartományba esik a dobott fejek száma?
A tartományt úgy add meg, hogy a fejek átlagos számára, vagyis az 50-re szimmetrikus legyen!
- KÉRDÉS
100 pénzérme-dobás esetén a legvalószínűbb eredmény az, hogy összesen 50-szer dobok fejet.
Mennyi ennek a valószínűsége?
VÁLASZ: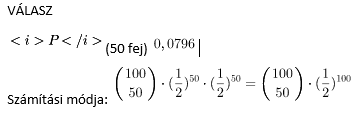
- KÉRDÉS
Jól látható, hogy a várható érték (50 fej) körüli fejek dobásának valószínűsége csak kevéssé tér el az 50 fej dobásának valószínűségétől.
Mekkora a valószínűsége annak, hogy a fejek száma 47 és 53 közé esik (beleértve a két határt is)?
VÁLASZ:0,5159 - KÉRDÉS
Mire érdemesebb fogadni: arra, hogy 47 és 53 közé esik (7 lehetséges kimenetel) vagy arra, hogy nem (94 lehetséges kimenetel)?
VÁLASZ:Arra, hogy 47 és 53 közé esik. - KÉRDÉS
Vizsgáld meg azokat az intervallumokat, amelyeknek az alsó és felső határa a várható értéktől (50 fej) egyenlő távolságra van, tehát az 50-re szimmetrikusak!- 100 dobásból milyen értékek közé esik a fejek száma legalább
 valószínűséggel?
valószínűséggel? - Mekkora az intervallum határának eltérése az 50-től?
- Nézd meg 100, 500 és 1000 dobás esetén is? Vesd össze az eltéréseket a fejek számának szórásával!
VÁLASZ:- 45 és 55 közé.
- 5 az eltérés, ami éppen a fejek számának szórása.
- Az eltérés minden esetben megegyezik a szórással.
- 100 dobásból milyen értékek közé esik a fejek száma legalább
- KÉRDÉS
Mekkora az eltérés legalább 95%-os valószínűség esetén 100, 500 és 1000 pénzfeldobás esetén?
Vesd össze az eltéréseket a fejek számának szórásával!
VÁLASZ:Az eltérés minden esetben megegyezik a szórás kétszeresével. - KÉRDÉS
Mekkora a valószínűsége annak, hogy a fejek száma a várható értéktől legfeljebb a szórás háromszorosával tér el? (100, 500, 1000 feldobás esetén)
VÁLASZ:A valószínűség minden esetben 0,997-nél nagyobb. - KÉRDÉS
A következőkben vizsgáljuk azokat az eseményeket, amelyek a dobott fejek számát adják meg. (Ha a véletlen kísérlet n dobásból áll, akkor a dobott fejek száma
0, 1, 2, …, n lehet, tehát n + 1 eseményt vizsgálunk.)- Jól látható, hogy 1000 dobás esetén több mint 0,997-et (99,7%-ot) kapunk, ha összegezzük azon események valószínűségeit, amelyeknél a dobott fejek száma a várható értéktől legfeljebb 3 szórásnyival tér el. Ezen események száma hány százalékát adja az összes vizsgált eseménynek?
- 100 dobás esetén az összes vizsgált eset hány százalékában teljesül, hogy a dobott fejek száma a várható értéktől legfeljebb háromszoros szórásnyira tér el?
- Mire lehet következtetni még több dobás esetén?
VÁLASZ:- Mivel a dobott fejek számára 1001 lehetőség van (ennyi tehát a vizsgált események száma), és az eltérés (vagyis a szórás háromszorosa) 48, ezért a kérdezett események száma 97, tehát az arány 9,7%.
- 2*15+1=31 Ez az összes vizsgált esemény számának a 31%-a.
- Minél több dobásból áll a kísérlet, arányaiban annál kevesebb vizsgált esemény együttes valószínűsége haladja meg a 99,7%-ot. Másképpen fogalmazva, minél több dobásból áll a véletlen kísérlet, annál kevésbé valószínű, hogy a kísérletben a dobott fejek száma „nagyon eltér” a várható értéktől (vagyis a „szélsőséges eredmény” bekövetkezésének valószínűsége kicsi). A „szélsőséges eredmény” itt azt jelenti, hogy a dobott fejek száma a várható értéktől 3 szórásnyinál is jobban eltér. A „szélsőséges eredmény” fogalma a kísérletek számától függ, 1000 dobás esetén például szélsőséges az a kísérleti eredmény (a három szórásnyinál nagyobb eltérést szélsőségesnek tekintve), amelyben az összes fejek száma kevesebb 452-nél vagy több 548-nál.