GEOMATECH tananyagok

KERESÉS

Felhasználói leírás

Gondoltam egy számot, hozzáadtam hetet, megszoroztam kettővel, majd az egészet kivontam százból. Végeredményül 66-ot kaptam. Melyik volt a gondolt szám?
Vizsgáld meg az interaktív alkalmazás segítségével pár ismert függvény grafikonjának az x = y tengelyre vett tükörképét! Hogyan kapcsolódik ez az eljárás az előbbi feladathoz? Hasonlítsd össze az inverzeket a tükörképekkel! Vizsgáld meg a tükrözéseket és inverzeket intervallumon megadott függvény esetén is! Mely esetekben van egyezés, és melyekben nincs, vagy csak részben van? A nem egyezők közül melyik javítható valamilyen egyszerű módosítással, például eltolással?

Tanácsok az interaktív alkalmazás használatához

Bal oldalt választhatunk függvénytípust, vagy adhatunk meg tetszőlegest. Minden függvényt tükrözhetünk, vehetjük inverzüket. Intervallumra csak a beépített függvényeket tudjuk szűkíteni. Mivel ilyenkor a csúszkák lassítják a programot, választható, hogy akarjuk-e ezeket használni. Lehetőségünk van megjeleníteni a segédfüggvényt, mely az aktuális függvény alapfüggvénye.

Feladatok

1. Vizsgáld meg először a lineáris, a páratlan kitevőjű hatvány, majd az exponenciális és logaritmus függvények tükörképeit! Pipáld be a Tükrözés jelölőnégyzetet! Például a következő függvényeket:
   
   
   INFORMÁCIÓ:

   A $\sqrt[x]{x}$ függvényt a „Képlet megadása” fülön tudjuk létrehozni, hatványfüggvényként beírva n értékére az $\frac{1}{3}$ -ot, a program kerekíteni fog. Olyan függvénypárokat adjunk meg, melyek egymás inverzei.
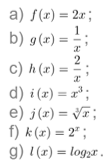
2. Vizsgáld meg az előbbi függvények inverzeit! Pipáld be az Inverz jelölőnégyzetet! Mit veszel észre?
   
   INFORMÁCIÓ:

   Az inverz – tükörkép megfeleltetés várható, semmiképp ne zárjuk az órát ennek rendbetétele nélkül!
3. Vizsgáld meg az előbbi függvényeket és inverzeiket egy-egy intervallumra szűkítve is! Pipáld be az Intervallum jelölőnégyzetet! Ha a rajzlapon szeretnéd beállítani az intervallumot, pipáld be az újonnan megjelenített csúszkák jelölőnégyzetet. Ez némiképp lassítja a programot. Milyen megszorítást jelent ez az inverzfüggvényre nézve?
   
   INFORMÁCIÓ:

   Az értelmezési tartomány és az értékkészlet szerepének felcserélődését várjuk.
4. Hasonlítsd össze a következő függvények tükörképeit az inverzeikkel:
   
   
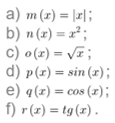
   INFORMÁCIÓ:

   Az inverz jelentése elkülönül a tükörképtől, mutassunk rá több példát! A választ már a négyzetgyök függvénynél megsejthetik.
5. Vizsgáld meg, hogyan hatnak az inverzekre az ismert függvénytranszformációk! Használd a csúszkákat, vagy a mellettük lévő beviteli mezőket! Ha intervallumra szűkítve szeretnéd használni a csúszkákat, pipáld be a csúszkák jelölőnégyzetet. Figyelem! Ez igen lassú lehet, légy türelemmel, ha ezt választod.
   
   INFORMÁCIÓ:

   Az eltolások és nyújtások koordinátánkénti felcserélését várjuk. Hozzuk összhangba ezt és a 3. feladat során tett észrevételt a felcseréléssel kapcsolatban!
6. Vizsgáljuk meg a trigonometrikus függvények inverzeit és tükörképeit egy-egy periódusra, félperiódusra szűkítve is! Mozgathatod az intervallum széleit jelző pontokat, de meg is adhatod azokat a Kezdőpont, illetve Végpont beviteli mezők segítségével!
   
   INFORMÁCIÓ:

   Azt várjuk, hogy a megfelelően szűk intervallum megtalálása után már egyezést látnak a tanulók. Ha az intervallumot máshol jelöljük ki, láthatóvá válik számukra is, hogy csupán megegyezésen alapul, melyik tükörképet használjuk.