GEOMATECH tananyagok

KERESÉS

Felhasználói leírás

Pitagorasz tételét egy speciális tangram készlet segítségével bizonyítjuk be.
Egy derékszögű háromszög oldalaira négyzeteket emeltünk. Helyezd el a befogóira emelt négyzeteket az átfogóra emelt négyzetbe hézagmentesen!
Az átfogó végpontjaiban található kék színű rombuszok segítségével változtathatóak a derékszögű háromszög befogói. Válassz ki egy tetszőleges beállítást, majd kattints a „Háromszög rögzítése” jelölőnégyzetbe!
A rögzítéssel egy időben a befogókra emelt négyzeteket kisebb darabokra osztottuk. Fogd meg a pirosra színezett darabokat, és húzd az átfogóra emelt négyzetbe!
Pitagorasz tételét úgy próbáld meg bizonyítani, hogy fedd le a piros elemekkel hézag és átfedés mentesen az átfogóra emelt négyzetet!
Segítségként használhatod az „Ellenőrzés” gombot, ezt megteheted akár elemenként is. Amint egy elem a „helyére” került, annak a színe ellenőrzéskor zöldre vált.
Mit jelent az, hogyha sikerül az átdarabolást elvégezni? Próbáld saját szavaiddal megfogalmazni a tételt!

Információ

A derékszögű háromszög befogóira emelt négyzetek területének összege egyenlő az átfogóra emelt négyzet területével.

Bizonyítás

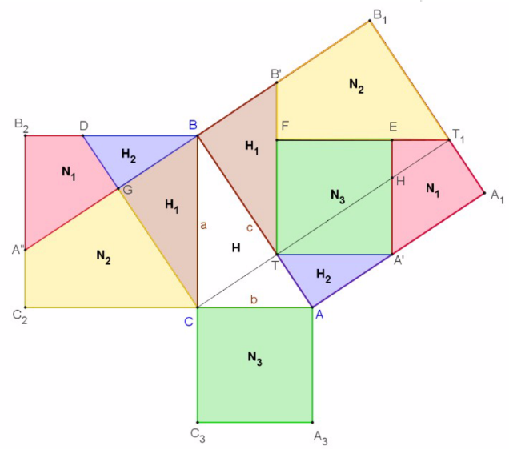
Az ábrán ABC derékszögű háromszög oldalaira szerkesztett négyzetek az AA₁B₁B, BB₂C₂C és a CC₃A₃A. Átdarabolással bizonyítjuk, hogy AA₁B₁B területe egyenlő a BB₂C₂C és CC₃A₃A négyzetek területének összegével.
Az AB oldalhoz tartozó magasság talppontja T, a CT egyenes T₁ pontban metszi az A₁B₁ oldalt. A’’ a B₂C₂ oldalon, A’ az AA₁, B’ a B₁Boldalon van, D a BB₂-n úgy, hogy:
CD AB, BA’’  AB, TA’  AC, TB’  CB.
G pont a C és BA’’ metszéspontja. F a T₁ pontból a TB’-re állított merőleges talppontja. E az A’ pontból a T₁F-re állított merőleges talppontja. H a TT₁ és az A’E szakaszok metszéspontja.
Ezekből következik, hogy az ábrán minden szakasz párhuzamos az eredeti háromszög valamelyik oldalával vagy magasságával:
AB  CD  CG  GD  AT  TB  A₁B₁  T₁B₁;
BC  TB’  C₂B₂  C₂A’’  A’’B  TF  FB’  A’E  A’H  HE;
CA  C₃A₃  C₂C  BB₂  BD  DB₂  A’T  T₁F  T₁E  EF;
CT  AA₁  BB₁  TT₁  BA’’  AA’  A’A₁  BB’  B’B₁  TH  HT₁  A’’G  GB.
Bebizonyítjuk, hogy az ábrán azonos színnel jelölt síkidomok egybevágók.

1. ... DGB  egybevágóak, mert mindkettő egybevágó az ATC -gel. Mivel TA’  AC és AA’  CT, mert mindkettő merőleges AB-re, AA’TC paralelogramma. Így TAA’ és ATCD valóban egybevágóak, mert AA’=CT, A’T=AC és A’AT=ATC=90°. Mivel a C pontnál két derékszög van, így A, C és C₂ egy egyenesen vannak, így AC és BD is párhuzamosak, ezért ABDC is paralelogramma, tehát az ABC  és a DGB  is egybevágók.
   Az ABC magassága CT és DCB magassága BG, tehát DGB is egybevágó TAA’-gel.
2. Hasonlóan bizonyítható, hogy a CBG és a TB’B is egybevágó.
3. FT₁B₁T’ négyszög egybevágó CGA’C₂ négyszöggel, mert CT₁G₁B téglalapban CG=T₁B₁, CC₂=T₁F=BC az ABC és a TT₁F háromszögek egybevágósága miatt (AB=TT₁ és a két háromszög megfelelő szögei is egyenlőek (mert merőleges szárú szögek), valamint a két négyszög szögei is egyenlőek (mert párhuzamos szárú szögek). A két négyszögben ugyanis a megfelelő oldalak párhuzamosak. A további két megfelelő oldalpár egyenlősége ezekből már következik.
4. Az A’A₁T₁E és A’’GDB₂ négyszögekben is párhuzamosak a megfelelő oldalak, így itt is elég bizonyítani, hogy A’A₁=GA’’ és A₁T₁=GD. A BB₂A’’ egybevágó az ABC-gel, mert BB2=BC és a megfelelő szögek pedig egyenlők, mert merőleges szárú szögek. Ebből azonban következik, hogy AA₁=BA’’.
   Mivel fentebb már beláttuk, hogy AA’=GB, ezért A’A₁=AA₁-AA’=BA’’-BG=GA.
   Már láttuk, hogy AT=GD, de AA₁T₁T téglalapban AT=A₁T₁, tehát A₁T₁=GD.
   A CC₃A₃A négyszög egybevágó az A’EFT négyszöggel. Mivel a megfelelő oldalak itt is párhuzamosak, a szögek valóban egyenlőek (derékszögek).
   CC₃A₃A egy négyzet, amelynek oldalai AC hosszúak. Már láttuk, hogy A’T=AC.
   Az ABCD és a TT₁F egybevágók, mert AB=TT₁ és ACB =TFT=90°, továbbá CAB=FTT₁, mert merőleges szárú szögek: TF  CB ebből következik, hogy TF AC és AB TT₁. Az egybevágóságból következik, hogy TF=AC, tehát A’EFT is AC oldalhosszúságú négyzet.

Tanácsok az interaktív alkalmazás használatához

Adott egy derékszögű háromszög az oldalai fölé emelt négyzetekkel. A „Háromszög rögzítése” feliratú jelölőnégyzet bekapcsolása után az elmozgatható (piros) síkidomokkal kell az átfogóra emelt négyzetet hézag és átfedés mentesen kitölteni. Bárhol megfogva mozgathatjuk őket szükség szerint.
Az „Ellenőrzés” jelölőnégyzet bekapcsolásakor a helyükre került elemek színe zöldre vált.
Az „Újra” gomb megnyomásával a kiindulási állapottól kezdhetjük újra a próbálkozást.

EMBED