11. évfolyam
Találkozás (geometriai valószínűség)
Szükséges előismeret
Geometriai valószínűség fogalma. Háromszög és négyzet területének számítása.
Az alkalmazás nehézségi szintje, tanárként
Könnyű, nem igényel külön készülést.
Módszertani megjegyzés, tanári szerep
A feladattípus ismert, valószínűleg sokan találkoztak már vele. Az érdeklődő diákoknak érdemes megmutatni, mert modellértékű. Közép- és általános iskolai tanulmányaik során többnyire kombinatorikus valószínűségi feladatokkal találkoznak. Íme egy példa, amikor másképp célszerű gondolkodni.
Érdemes a modellt mindenképpen közösen kialakítani, főképp, ha nem találkoztak még ilyen jellegű feladattal a diákok. A tanegység több szinten nyújt segítséget a feldolgozásban, igazán tehetséges tanulók esetében innentől maguk is próbálkozhatnak, de tanári demonstrációként is használhatjuk.
Felhasználói leírás
MILYEN ESÉLLYEL TALÁLKOZIK A KÉT BARÁT?
Adott az alapprobléma: vajon milyen eséllyel találkozik a két fiú vásárlás közben? Ismerjük szokásaikat. Tudjuk, hogy mindketten ugyanannyi időt töltenek vásárlással ugyanabban a boltban (persze, ha bezár a bolt, akkor nekik is távozniuk kell, ilyenkor nem tudnak feltétlenül ugyanannyi időt tölteni vásárlással.)
De hogy jön ide egy koordináta-rendszerben felvett négyzet? Mit jelentenek a pontjai? Hogyan segít ez megtalálni a kérdésre a választ?
Tanácsok az interaktív alkalmazás használatához
A csúszkákkal állíthatjuk a paramétereket:
-
- milyen időintervallumban van nyitva a bolt,
- mennyi időt töltenek alkalmanként a boltban.
Jelölőnégyzet segítségével beállíthatjuk, hogy a fiúk érkezését reprezentáló pont nyomot hagyjon-e.
Szintén jelölőnégyzettel érhetjük el, hogy a pont szerepének értelmezéséhez összekapcsoljuk a koordináták jelentésével (érkezések megjelenítése).
EMBED
Feladatok
- Mit jelent a pont két koordinátája? Kiinduló ábránkon a négyzet oldala 1 órányi időtartamnak felel meg.
INFORMÁCIÓMegoldás: A fiúk boltba érkezésének idejét.
- Mit jelent, ha a pont kék nyomot hagy? És mit jelent, ha zöldet?
INFORMÁCIÓMegoldás: Ha kék, akkor nem fognak találkozni, ha zöld, akkor igen.
- Mi változik az ábrán, ha a bolt nyitva tartását növeled?
INFORMÁCIÓMegoldás: Az ábrán csak a felirat változik, mert a négyzet oldala a bolt nyitva tartását reprezentálja, a nagysága nem arányos az időtartammal. Viszont a négyzeten belül minden arányosan változik.
- Mit változtat a kiindulási ábrán, ha a fiúk vásárlásának idejét növeled?
INFORMÁCIÓMegoldás: A segítségek bekapcsolása nélkül semmi. A 3. lépésben (egyik jön – másik megy) változik a „jó” pontokat tartalmazó síkidom.
- Lehetséges-e úgy változtatni a nyitva tartást és a vásárlás idejét, hogy a találkozás valószínűsége 0 legyen? Gondold végig, hogy kellene ennek látszania az ábrán!
INFORMÁCIÓMegoldás: Nem. Esetleg érdemes megemlíteni, hogyha a vásárlás idejét 0-ra állíthatnánk (ami persze most nem életszerű, és ezért be sem állítható), akkor a „sáv” helyett a négyzet átlója reprezentálná a „jó” pontokat. A szakasz területe nulla, tehát a valószínűség is. Azonban mégsem lehetetlen a találkozás, hiszen ha pontosan egyszerre lépnek be, akkor mégis összefutnak.
- Mennyi annak a valószínűsége, hogy a két fiú egyszerre lép a boltba? Hol helyezkednek el azok a pontok, melyek ezt az esetet reprezentálják?
INFORMÁCIÓMegoldás: A négyzet átlóján lesznek a megfelelő pontok. A kérdés az előzővel azonos meggondolással válaszolható meg. Érdemes előre elgondolni, hogy melyik verzióban hangozzon el. Bizonyos esetekben a megértés ellenőrzésére a másik megfogalmazásban is feltehetjük a kérdést például házi feladatként.
-
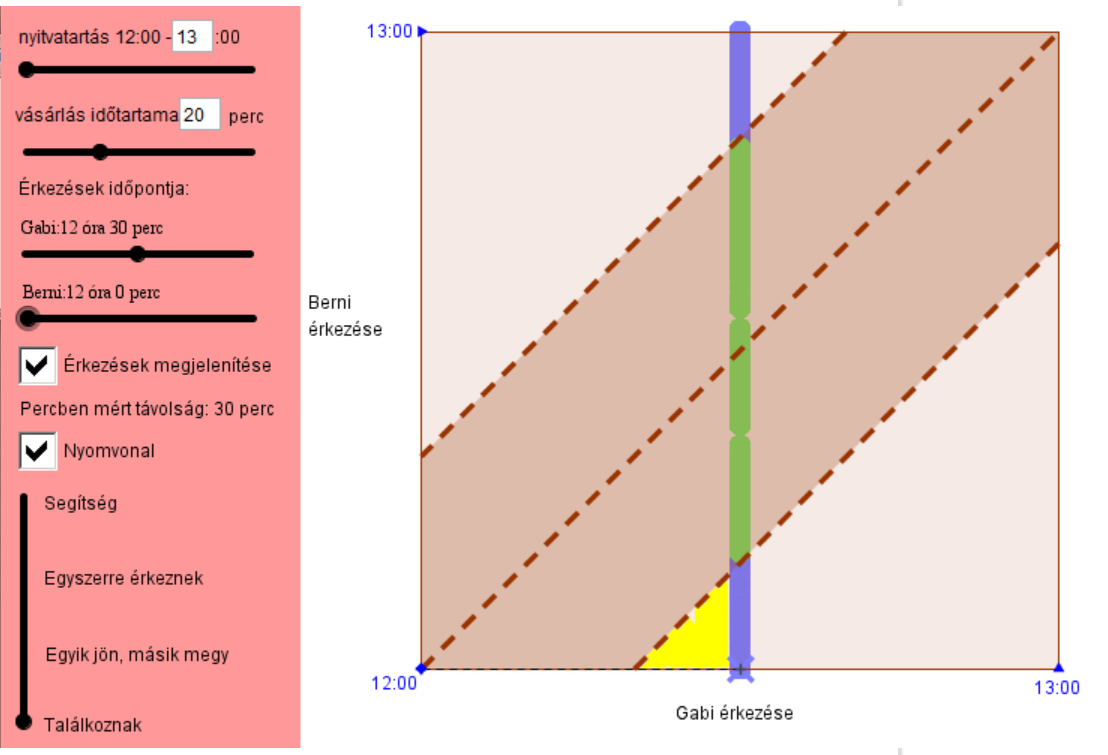
Tekintsük a következő beállítást:
- a bolt 12-től 13 óráig tart nyitva (tehát 1 óra időtartamot)
- Gabi 12:30-kor érkezik
- 20 percig vásárolnak.
INFORMÁCIÓMegoldás: Egy szakaszt kellene kapni a négyzet oldalával párhuzamosan. Ha a kísérletezést irányítottabban szeretnénk lebonyolítani, akkor szóljunk előre, hogy ne a pontot mozgassák, hanem a csúszkán változtassák a megfelelő értéket.
Az ábrán segítségként sárgával jelölt háromszög befogói 10 percet reprezentálnak, tehát a négyzet oldalának hatoda a hosszuk. Két ilyen kék szakasz az oldal két hatodát adja összesen, vagyis a zöld szakasz négy hatoda az egésznek, ami egyben a valószínűség is.