Fizika (7-8.)
A Cartesius -búvár működése - kalibráljuk a búvárt vízzel!
Módszertani célkitűzés
Ennek a tananyagegységnek a segítségével a Cartesius-búvár működését mutathatjuk be.
Az alkalmazás nehézségi szintje, tanárként
Könnyű, nem igényel külön készülést.
Módszertani megjegyzések, tanári szerep
###
Felhasználói leírás
Ez a tananyagegység a Cartesius-búvár működését mutatja meg részletesen, a középiskolások számára.
Bevezető, ráhangolódás
Vizsgáld meg a folyadékba merülő testek lehetséges egyensúlyi állapotait!
Mi történik a testtel az alábbi esetekben?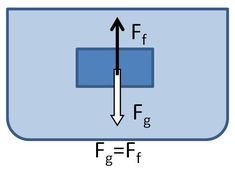
A folyadékba merülő test egyensúlyi helyzete a folyadékfelszínhez képest a testre ható gravitációs erő és a felhajtóerő viszonyától függ.
Ha a testre ható nehézségi erő és felhajtóerő nagysága megegyezik, akkor a testre ható erők eredője nulla, ezért a test nyugalomban marad. Vagyis bármilyen mélyre nyomjuk a víz felszíne alá, helyzetét nem változtatja meg, a test lebeg.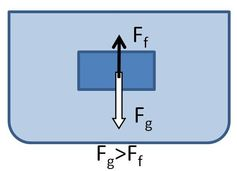
Ha a testre ható gravitációs erő nagyobb a felhajtóerőnél, a test a nagyobb gravitációs erő hatásvonalában, annak irányában mozdul el, vagyis a test lesüllyed.
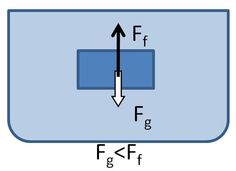
Ha a testre ható gravitációs erő kisebb a felhajtóerőnél, az eredő erő felfelé mutat, így a test a nagyobb felhajtóerő hatásvonalának irányában felfelé mozdul el, a felszínre tör. A test addig emelkedik ki a folyadékból, míg a rá ható gravitációs erő és a felhajtóerő egyenlő nem lesz. Az egyensúly bekövetkezésekor a test úszik. Az úszás a folyadékba részben bemerült testnek az az egyensúlyi állapota, amelyben a testre ható gravitációs erő egyenlő a test folyadékba merülő részére ható felhajtóerővel.
A cartesius-búvár működése - kalibráljuk a búvárt vízzel!
A szimuláció segítségével megvizsgálhatod és értelmezheted a híres Cartesius-búvár működését, mely a folyadékba merülő testek lehetséges egyensúlyi állapotait modellezi.
Feladatok
- FELADAT
Figyeld meg a bejelentkező képernyőt! Mit látsz a képen? - FELADAT
Figyeld meg a búvár viselkedését!- Állítsd a kezdeti értéknél nagyobbra a legelső csúszkát! Mit tudsz változtatni a segítségével?
- Mi történik, ha megnyomod a palack oldalát?
- Mit tapasztalsz, ha megnöveled a nyomást?
- Mi történik, ha alámerülő búvárnál csökkented a nyomást?
- Változik-e a búvárban lévő vízszint a palack oldalát megnyomva?
- FELADAT
Figyeld a kísérleti összeállítás melletti vektorábrát!- Milyen erők hatnak a búvárra? Mit jelöl és milyen irányú az , az és az ?
- Változnak-e és ha igen, hogyan, a búvár mozgása közben a rá ható erők?
- Figyelve az erők nagyságát, mit mondhatunk a búvárra ható erők eredőjéről a búvár különböző helyzeteiben? Milyen mozgást végez a búvár az egyes esetekben?
- FELADAT
Értelmezd a tapasztaltakat!- Miért növekedik a búvárbeli vízszint a palack oldalát megnyomva?
- A vezérlőpanel jobb alsó sarkában láthatod a búvár átlagos sűrűségét (). Hogyan és miért változik az értéke a nyomást változtatva?
- Mikor láthatjuk pirossal a búvár átlagos sűrűségét?
- Mitől függ a búvár viselkedése a palackban, azaz mikor merül el, illetve mikor úszik?
- Mitől függ a felhajtóerő nagysága?
- Miért változik mozgás közben a búvárra ható felhajtóerő nagysága?
- FELADAT
A nyomás melletti csúszka segítségével állíthatod a búvárban kezdetben lévő levegő térfogatát (Vb0). Változtasd értékét és figyeld meg a búvár viselkedését! - FELADAT
Az gombbal állítsd vissza a kiinduló helyzetet!- A nyomás alatti csúszka (h) segítségével indítsd a víz alól a búvárt (állítsd 0 cm-nél nagyobbra, de a maximálisnál kisebbre a h értékét), majd figyeld meg, mi történik!
- Vidd a búvárt a palack legaljára (azaz állítsd a csúszka értékét a maximálisra)! Mi történik?
LEHETSÉGES HÁZI FELADAT
Készíts otthon jól működő Cartesius-búvárt ásványvizes palackból és cseppentőből!
SZEMCSEPPENTŐS CARTESIUS-BÚVÁR KÉSZÍTÉSE
KAPCSOLÓDÓ ÉRDEKESSÉGEK
A Cartesius-búvár feltalálását Renatus Cartesius-nak tulajdonítják, aki nem más, mint René Descartes latinosított néven. 1596-tól 1650-ig élt, neves francia filozófus, természetkutató és matematikus volt.
Fizikai munkásságát elsősorban az optika és a mechanika terén fejtette ki. Descartes nevéhez fűződik a fénytörés elmélete (Snellius-Descartes-féle törvény), gyakorlati útmutatást adott a lencsék célszerű csiszolására.
Matematikai munkássága is igen jelentős. Különösen fiatal éveiben szeretett matematikával foglalkozni. Megalapította a koordináta geometriát, és tovább fejlesztette az algebrai egyenletek elméletét.
Descartes a racionalizmust hirdette. Minden lehetséges dologban kételkedett, még magában a világban is. Arra a következtetésre jutott, hogy csak egy dolog van, amiben nem kételkedhet, hogy az a dolog, ami kételkedik, tehát gondolkozik, az létezik. 23 éves korában fogalmazta meg egyik leggyakrabban idézett mondását: Cogito ergo sum. (Gondolkodom, tehát vagyok.)